Lecture 1: Probability and Counting
Stat 110, Prof. Joe Blitzstein, Harvard University
Definitions
We start with some basic definitions:
Definition: sample space
A sample space is the set of all possible outcomes of an experiment.
Definition: event
An event is a subset of the sample space.
Definition: naïve definition of probability
Under the naïve definition of probability, the probability of a given event $A$ occurring is expressed as
\begin{align} P(A) &= \frac{ \text{# favorable outcomes}}{\text{# possible outcomes}} \end{align}
assuming all outcomes are equally likely in a finite sample space.
Counting
With the multiplication rule, if we have an experiment with $n_1$ possible outcomes; and we have a 2nd experiment with $n_2$ possible outcomes; …, and for the rth experiment there are $n_r$ possible outcomes; then overall there are $n_1 n_2 … n_r$ possible outcomes (product).
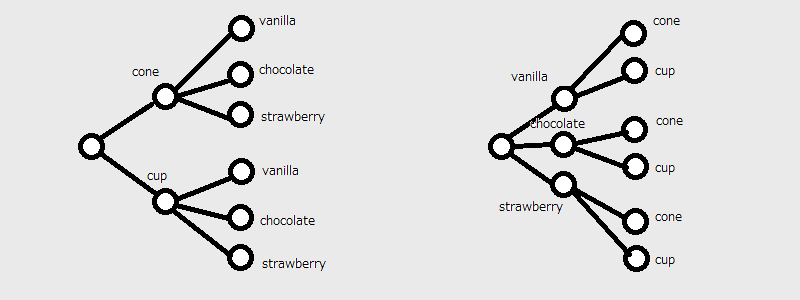
Let’s say you are ordering ice cream. You can either get a cone or a cup, and the ice cream comes in three flavors. The order of choice here does not matter, and the total number of choices is $2 \times 3 = 3 \times 2 = 6$. This can be represented with a very simple probability tree.
The binomial coefficient is defined as
\begin{align} \binom{n}{k} = \begin{cases} \frac{n!}{(n-k)!k!} & \quad \text{if } 0 \le k \le n \newline 0 & \quad \text{if } k \gt n \end{cases} \end{align}
This expresses the number of ways you could choose a subset of size $k$ from $n$ items, where order doesn’t matter.
Sampling
Choose $k$ objects out of $n$
| ordered | unordered | |
|---|---|---|
| w/ replacement | $n^k$ | ??? |
| w/o replacement | $n(n-1)(n-2) \ldots (n-k+1)$ | $\binom{n}{k}$ |
- ordered, w/ replacement: there are $n$ choices for each $k$, so this follows from the multiplication rule.
- ordered, w/out replacement: there are $n$ choices for the 1st position; $n-1$ for the 2nd; $n-2$ for the 3rd; and $n-k+1$ for the $k$th.
- unordered, w/ replacement: ???
- unordered, w/out replacement: the binomial coefficient; think of choosing a hand from a deck of cards.
Out of the 4 ways of choosing $k$ objects out of $n$, the case of unordered, with replacement is perhaps not as clear-cut and easy to grasp as the other three. Move on to Lecture 2.
View Lecture 1: Probability and Counting | Statistics 110 on YouTube.
Lecture 2: Story Proofs, Axioms of Probability
Sampling, continued
Choose $k$ objects out of $n$
| ordered | unordered | |
|---|---|---|
| w/ replacement | $n^k$ | ??? |
| w/o replacement | $n(n-1)(n-2) \ldots (n-k+1)$ | $\binom{n}{k}$ |
- ordered, w/ replacement: there are $n$ choices for each $k$, so this follows from the multiplication rule.
- ordered, w/out replacement: there are $n$ choices for the 1st position; $n-1$ for the 2nd; $n-2$ for the 3rd; and $n-k+1$ for the $k$th.
- unordered, w/ replacement: we will get to this shortly…
- unordered, w/out replacement: the binomial coefficient; think of choosing a hand from a deck of cards.
To complete our discussion of sampling, recall that of the four ways of sampling as shown above, all except the case of unordered, with replacement follow immediately from the multiplication rule.
Now the solution is $\binom{n+k-1}{k}$, but let’s see if we can prove this.
A simple proof
We start off with some simple edge cases.
If we let $k=0$, then we are not choosing anything, and so there is only one
solution to this case: the empty set.
\begin{align}
\text{let }k = 0 \Rightarrow \binom{n+0-1}{0} &= \binom{n-1}{0} \
&= 1
\end{align}
If we let $k=1$, then there are $n$ ways we could select a single item out of a
total of $n$.
\begin{align}
\text{let }k = 1 \Rightarrow \binom{n+1-1}{1} &= \binom{n}{1} \
&= n
\end{align}
Now let’s consider a simple but non-trivial case. If we let $n=2$, then
\begin{align}
\text{let }n = 2 \Rightarrow \binom{2+k-1}{k} &= \binom{k+1}{k} \
&= \binom{k+1}{1} \
&= k+1
\end{align}
Here’s an example of $n=2, k=7$:

But notice that we are really doing here is placing $n-1$ dividers between $k$ elements. Or in other words, we are choosing $k$ slots for the elements out of $n+k-1$ slots in total.
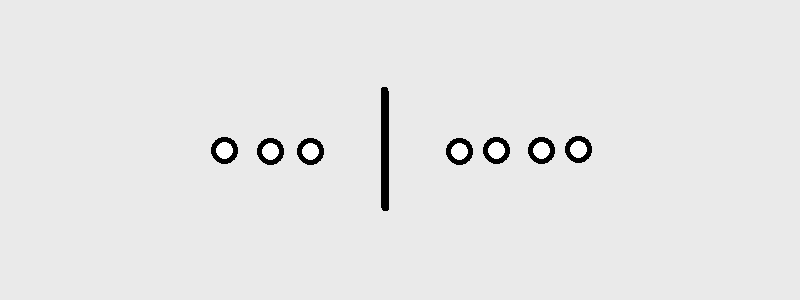
And we can easily build on this understanding to other values of $n$ and $k$.
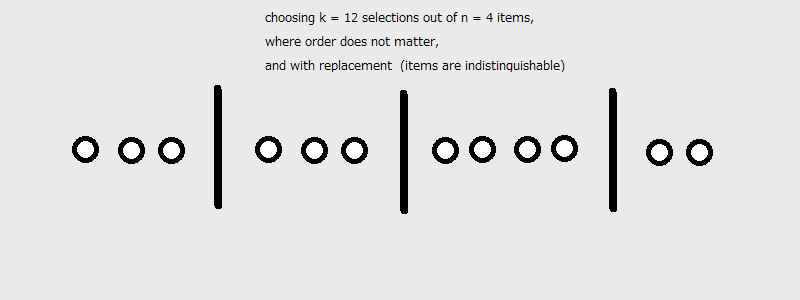
And the number of ways to select $k$ items out of $n$, unordered and with replacement, is:
\begin{align}
\text{choose k out n items, unordered, with replacement} &=
\binom{n+k-1}{k} \
&= \binom{n+k-1}{n-1}
\end{align}
Story Proof
A story proof is a proof by interpretation. No algebra needed, just intuition.
Here are some examples that we have already come across.
Ex. 1
\(\binom{n}{k} = \binom{n}{n-k}\)
Choosing $k$ elements out of $n$ is the same as choosing $n-k$ elements out of $n$. We’ve just seen this above!
Ex. 2
\(n \binom{n-1}{k-1} = k \binom{n}{k}\)
Imagine picking $k$ people out of $n$, and then designating of the $k$ as president. You can either select all $k$ people, and then choose 1 from among those $k$. Or, you can select a president, and then choose the remaining $k-1$ out of the $n-1$ people.
Ex. 3
\(\binom{m+n}{k} = \sum_{j=0}^{k} \binom{m}{j} \binom{n}{k-j}\)
Suppose you had $m$ boys and $n$ girls, and you needed to select $k$ children out of them all. You could do this by first choosing $j$ out of the $m$ boys, and then choosing $k-j$ of the girls. You would have to apply the multiplication rule to get the total number of combinations, and then sum them all up. This is known as Vandermonde’s identity.
Non-naïve Definition of Probability
Now we move from the naïve definition of probability into the more abstract and general.
Definition: non-naïve definition of probability
Let $S$ be a sample space, the set of all possible outcomes of some experiment. $S$ might not be finite anymore, and all outcomes might not be equally probable, either.
Let $A$ be an event in, or a subset of, $S$.
Let $P$ be a function that maps an event $A$ to some value from $0$ to $1$.
And we have the following axioms:
Axiom 1
\begin{align} P(\emptyset) = 0 \
P(\Omega) = 1 \end{align}
The probability of the empty set, or a null event, is by definition $0$.
The probability of the entire space is by definition $1$.
These are the 2 extremes, and this is why Prof. Blitzstein lumps them together in one rule.
Axiom 2
\[P(\bigcup_{n=1}^{\infty} A_{n}) = \sum_{n=1}^{\infty} P(A_{n}) \iff A_1, A_2, ... A_n \text{ are disjoint (non-overlapping)}\]
Every theorem about probability follows from these 2 rules. You might want to have a look at Kolmogorov’s axioms.
View Lecture 2: Story Proofs, Axioms of Probability | Statistics 110 on YouTube.
Lecture 3: Birthday Problem, Properties of Probability
The Birthday Problem
Given $k$ people, what is the probability of at least 2 people having the same birthday?
First, we need to define the problem:
- there are 365 days in a year (no leap-years)
- births can be on any day with equal probability (birthdays are independent of one another)
- treat people as distinguishable, because.
$k \le 1$ is meaningless, so we will not consider those cases.
Now consider the case where you have more people than there are days in a year. In such a case,
\[P(k\ge365) = 1\]Now think about the event of no matches. We can compute this probability using the naïve definition of probability:
\[P(\text{no match}) = \frac{365 \times 364 \times \cdots \times 365-k+1}{365^k}\]Now the event of at least one match is the complement of no matches, so
\begin{align}
P(\text{at least one match}) &= 1 - P(\text{no match})
&= 1 - \frac{365 \times 364 \times \cdots
\times 365-k+1}{365^k}
\end{align}
import numpy as np
DAYS_IN_YEAR = 365
def bday_prob(k):
def no_match(k):
days = [(DAYS_IN_YEAR-x) for x in range(k)]
num = np.multiply.reduce(days, dtype=np.float64)
return num / DAYS_IN_YEAR**k
return 1.0 - no_match(k)
print("With k=23 people, the probability of a match is {:0f}, already exceeding 0.5.".format(bday_prob(23)))
print("With k=50 people, the probability of a match is {:0f}, which is approaching 1.0.".format(bday_prob(50)))
Properties
Let’s derive some properties using nothing but the two axioms stated earlier.
Property 1
The probability of an event $A$ is 1 minus the probability of that event’s inverse (or complement).
\begin{align} P(A^{c}) &= 1 - P(A) \
\
\because 1 &= P(S) \
&= P(A \cup A^{c}) \
&= P(A) + P(A^{c}) & \quad \text{since } A \cap A^{c} = \emptyset ~~ \blacksquare \end{align}
Property 2
If $A$ is contained within $B$, then the probability of $A$ must be less than or equal to that for $B$.
\begin{align} \text{If } A &\subseteq B \text{, then } P(A) \leq P(B) \\
\
\because B &= A \cup ( B \cap A^{c}) \
P(B) &= P(A) + P(B \cap A^{c}) \
\
\implies P(B) &\geq P(A) \text{, since } P(B \cap A^{c}) \geq 0 & \quad \blacksquare \end{align}
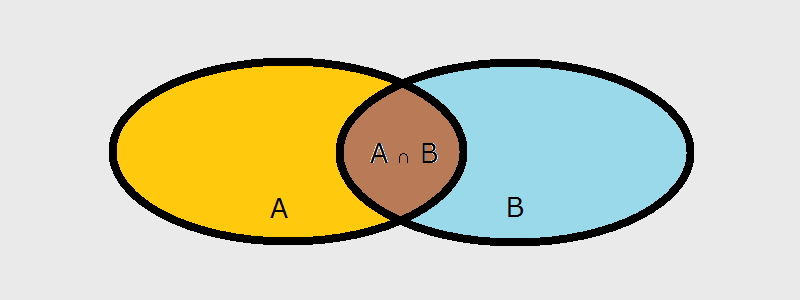
Property 3, or the Inclusion/Exclusion Principle
The probability of a union of 2 events $A$ and $B$
\begin{align} P(A \cup B) &= P(A) + P(B) - P(A \cap B) \
\
\text{since } P(A \cup B) &= P(A \cup (B \cap A^{c})) \
&= P(A) + P(B \cap A^{c}) \
\
\text{but note that } P(B) &= P(B \cap A) + P(B \cap A^{c}) \
\text{and since } P(B) - P(A \cap B) &= P(B \cap A^{c}) \
\
\implies P(A \cup B) &= P(A) + P(B) - P(A \cap B) ~~~~ \blacksquare \end{align}
This is the simplest case of the principle of inclusion/exclusion.
Considering the 3-event case, we have:
\begin{align} P(A \cup B \cup C) &= P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C) \end{align}
…where we sum up all of the separate events; and then subtract each of the pair-wise intersections; and finally add back in that 3-event intersection since that was subtracted in the previous step.
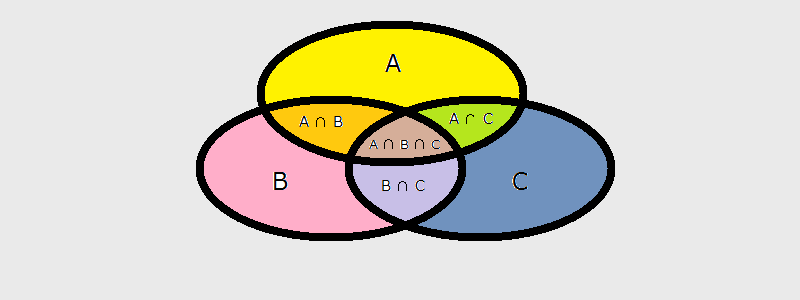
For the general case, we have:
\[P(A_1 \cup A_2 \cup \cdots \cup A_n) = \sum_{j=1}^n P(A_{j}) - \sum_{i<j} P(A_i \cap A_j) + \sum_{i<j<k} P(A_i \cap A_j \cap A_k) \cdots + (-1)^{n-1} P(A_1 \cap A_2 \cap \cdots \cap A_n)\]… where we
- sum up all of the separate events
- subtract the sums of all even-numbered index intersections
- add back the sums of all odd-numbered index intersections
de Montmort’s problem (1713)
Again from a gambling problem, say we have a deck of $n$ cards, labeled 1 through $n$. The deck is thoroughly shuffled. The cards are then flipped over, one at a time. A win is when the card labeled $k$ is the $k^{th}$ card flipped.
What is the probability of a win?
Let $A_k$ be the event that card $k$ is the $k^{th}$ card flipped. The probability of a win is when at least one of the $n$ cards is in the correct position. Therefore, what we are interested in is
\[P(A_1 \cup A_2 \cup \cdots \cup A_n)\]Now, consider the following:
\begin{align}
P(A_1) &= \frac{1}{n} & \quad \text{since all outcomes are equally likely}
\
P(A_1 \cap A_2) &= \frac{1}{n} \left(\frac{1}{n-1}\right) =
\frac{(n-2)!}{n!} \
&\vdots \
P(A_1 \cap A_2 \cap \cdots \cap A_k) &= \frac{(n-k)!}{n!} & \quad
\text{because, symmetry} \
\end{align}
Which leads us to:
\begin{align}
P(A_1 \cup A_2 \cup \cdots \cup A_k) &= \binom{n}{1}\frac{1}{n} -
\binom{n}{2}\frac{1}{n(n-1)} + \binom{n}{3}\frac{1}{n(n-1)(n-2)} - \cdots \
&= n \frac{1}{n} - \left(\frac{n(n-1)}{2!}\right)\frac{1}{n(n-1)} +
\left(\frac{n(n-1)(n-2)}{3!}\right)\frac{1}{n(n-1)(n-2)} - \cdots \
&= 1 - \frac{1}{2!} + \frac{1}{3!} - \frac{1}{4!} \cdots
(-1)^{n-1}\frac{1}{n!} \
&= 1 - \sum_{k=1}^{\infty} \frac{(-1)^{k-1}}{k!} \
&= 1 - \frac{1}{e} \
\
\text{ since } e^{-1} &= \frac{(-1)^0}{0!} + \frac{-1}{1!} +
\frac{(-1)^2}{2!} + \frac{(-1)^3}{3!} + \cdots + \frac{(-1)^n}{n!} ~~~~ \text{
from the Taylor expansion of } e^{x}
\end{align}
Appendix A: The Birthday Paradox Experiment
Here’s a very nice, interactive explanation of the Birthday Paradox.
View on Lecture 3: Birthday Problem, Properties of Probability | Statistics 110 on YouTube.
Lecture 4: Conditional Probability
Definitions
We continue with some basic definitions of independence and disjointness:
Definition: independence & disjointness
Events A and B are independent if $P(A \cap B) = P(A)P(B)$. Knowing that event A occurs tells us nothing about event B.
In contrast, events A and B are disjoint if A occurring means that B cannot occur.
What about the case of events A, B and c?
Events A, B and C are independent if
\begin{align} P(A \cap B) &= P(A)P(B), ~~ P(A \cap C) = P(A)P(C), ~~ P(B \cap C) = P(B)P(C) \
P(A \cap B \cap C) &= P(A)P(B)P(C) \end{align}So you need both pair-wise independence and three-way independence.
Newton-Pepys Problem (1693)
Yet another famous example of probability that comes from a gambling question.
We have fair dice. Which of the following events is most likely?
- $A$ … at least one 6 with 6 dice
- $B$ … at least two 6’s with 12 dice
- $C$ … at least three 6’s with 18 dice
Let’s solve for the probability of each event using independence.
\begin{align}
P(A) &= 1 - P(A^c) ~~~~ &\text{since the complement of at least one 6 is no
6’s at all}
&= 1 - \left(\frac{5}{6}\right)^6 &\text{the 6 dice are independent, so
we just multiply them all}
&\approx 0.665
P(B) &= 1 - P(\text{no 6’s}) - P(\text{one 6})
&= 1 - \left(\frac{5}{6}\right)^{12} - 12
\left(\frac{1}{6}\right)\left(\frac{5}{6}\right)^{11} &\text{… does this look
familiar?}
&\approx 0.619
P(C) &= 1 - P(\text{no 6’s}) - P(\text{one 6}) - P(\text{two 6’s})
&= 1 - \sum_{k=0}^{2} \binom{18}{k} \left(\frac{1}{6}\right)^k
\left(\frac{5}{6}\right)^{18-k} &\text{… it’s Binomial probability!}
&\approx 0.597
\end{align}
Conditional Probability
Conditioning is the soul of probability.
How do you update your beliefs when presented with new information? That’s the question here.
Consider 2 events $A$ and $B$. We defined conditional probability a $P(A|B)$, read the probability of A given B.
Suppose we just observed that $B$ occurred. Now if $A$ and $B$ are independent, then $P(A|B)$ is irrelevant. But if $A$ and $B$ are not independent, then the fact that $B$ happened is important information and we need to update our uncertainty about $A$ accordingly.
Definition: conditional probability
\begin{align} \text{conditional probability } P(A|B) &= \frac{P(A \cap B)}{P(B)} &\text{if }P(B)\gt0
\end{align}
Prof. Blitzstein gives examples of Pebble World and Frequentist World to help explain conditional probability, but I find that Legos make things simple.
Theorem 1
The intersection of events $A$ and $B$ can be given by
\begin{align} P(A \cap B) = P(B) P(A|B) = P(A) P(B|A) \end{align}
Note that if $A$ and $B$ are independent, then conditioning on $B$ means nothing (and vice-versa) so $P(A|B) = P(A)$, and $P(A \cap B) = P(A) P(B)$.
Theorem 2
\begin{align} P(A_1, A_2, … A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1,A_2)…P(A_n|A_1,A_2,…,A_{n-1}) \end{align}
Theorem 3: Bayes’ Theorem
\begin{align} P(A|B) = \frac{P(B|A)P(A)}{P(B)} ~~~~ \text{this follows from Theorem 1} \end{align}
Appendix A: Bayes’ Rule Expressed in Terms of Odds
The odds of an event with probability $p$ is $\frac{p}{1-p}$.
An event with probability $\frac{3}{4}$ can be described as having odds 3 to 1 in favor, or 1 to 3 against.
Let $H$ be the hypothesis, or the event we are interested in.
Let $D$ be the evidence (event) we gather in order to study $H$.
The prior probability $P(H)$ is that for which $H$ is true before we observe any new evidence $D$.
The posterior probability $P(H|D)$ is, of course, that which is after we observed new evidence.
| The likelihood ratio is defined as $\frac{P(D | H)}{P(D^c | H^c)}$ |
Applying Bayes’ Rule, we can see how the posterior odds, prior odds and likelihood odds are related:
\begin{align}
P(H|D) &= \frac{P(D|H)P(H)}{P(D)}
P(H^c|D) &= \frac{P(D|H^c)P(H^c)}{P(D)}
\Rightarrow \underbrace{\frac{P(H|D)}{P(H^c|D)}}{\text{posterior odds of
H}} &= \underbrace{\frac{P(H)}{P(H^c)}}{\text{prior odds of H}} \times
\underbrace{\frac{P(D|H)}{P(D|H^c)}}_{\text{likelihood ratio}}
\end{align}
Appendix B: Translating Odds into Probability
To go from odds back to probability
\begin{align} p = \frac{p/q}{1 + p/q} & &\text{ for } q = 1-p \end{align}
View Lecture 4: Conditional Probability | Statistics 110 on YouTube.
Lecture 5: Conditioning Continued, Law of Total Probability
Thinking conditionally is a condition for thinking.
How can we solve a problem?
- Try simple and/or extreme cases.
- Try to break the problem up into simpler pieces; recurse as needed.

Let $A_1, A_2, \dots, A_n$ partition sample space $S$ into disjoint regions that sum up to $S$. Then
\begin{align}
P(B) &= P(B \cap A_1) + P(B \cap A_2) + \dots + P(B \cap A_n)
&= P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + \dots + P(B|A_n)P(A_n)
\end{align}
Note that statistics is as much of an art as it is a science, and choosing the right partitioning is key. Poor choices of partitions may results in many, even more difficult to solve sub-problems.
This is known as the Law of Total Probability. Conditional probability is important in its own right, and sometimes we use conditional probability to solve problems of unconditional probability, as above with $P(B)$.
But conditional probability can be very subtle. You really need to think when using conditional probability.
Ex. 1
Let’s consider a 2-card hand drawn from a standard playing deck. What is the probability of drawing 2 aces, given that we know one of the cards is an ace?
\begin{align}
P(\text{both are aces | one is ace}) &= \frac{P(\text{both are
aces})}{P(\text{one is ace})}
&= \frac{P(\text{both are aces})}{1 - P(\text{neither is ace})}
&= \frac{\binom{4}{2}/\binom{52}{2}}{1 - \binom{48}{2}/\binom{52}{2}}
&= \frac{1}{33}
\end{align}
But now think about this: What is the probability of drawing 2 aces, knowing that one of the cards is the ace of spades?
\begin{align}
P(\text{both are aces | ace of spades}) &= P(\text{other card is also an
ace})
&= \frac{3}{51}
&= \frac{1}{17}
\end{align}
Notice how the fact that we know we have the ace of spades nearly doubles the probability of having 2 aces.
Ex. 2
Suppose there is a test for a disease, and this test is touted as being “95% accurate”. The disease in question afflicts 1% of the population. Now say that there is a patient who tests positive for this disease under this test.
First we define the events in question:
Let $D$ be the event that the patient actually has the disease.
Let $T$ be the event that the patient tests positive.
Since that phrase “95% accurate” is ambiguous, we need to clarify that.
\begin{align} P(T|D) = P(T^c|D^c) = 0.95 \end{align}
In other words, conditioning on whether or not the patient has the disease, we will assume that the test is 95% accurate.
What exactly are we trying to find?
| What the patient really wants to know is not $P(T | D)$, which is the accuracy of |
| the test; but rather $P(D | T)$, or the probability she has the disease given that |
| the test returns positive. Fortunately, we know how $P(T | D)$ relates to |
| $P(D | T)$. |
\begin{align}
P(D|T) &= \frac{P(T|D)P(D)}{P(T)} ~~~~ & &\text{… Bayes Rule}
&= \frac{P(T|D)P(D)}{P(T|D)P(D) + P(T|D^c)P(D^c)} ~~~~ & & \text{… by the
Law of Total Probability}
&= \frac{(0.95)(0.01)}{(0.95)(0.01) + (0.05)(0.99)} ~~~~ & & \text{… the
rarity of the disease competes with the rarity of true negatives}
&\approx 0.16
\end{align}
Common Pitfalls
-
Mistaking $P(A|B)$ for $P(B|A)$. This is also known as the Prosecutor’s Fallacy, where instead of asking about the probability of guilt (or innocence) given all the evidence, we make the mistake of concerning ourselves with the probability of the evidence given guilt. An example of the Prosecutor’s Fallacy is the case of Sally Clark.
-
Confusing prior $P(A)$ with posterior $P(A B)$. Observing that event $A$ occurred does not mean that $P(A) = 1$. But $P(A A) = 1$ and $P(A) \neq 1$. - Confusing independence with conditional independence. This is more subtle than the other two.
Definition
Events $A$ and $B$ are conditionally independent given event $C$, if
\begin{align} P(A \cap B | C) = P(A|C)P(B|C) \end{align}
In other words, conditioning on event $C$ does not give us any additional information on $A$ or $B$.
_Does conditional independence given $C$ imply unconditional independence? _
Ex. Chess Opponent of Unknown Strength
Short answer, no.
Consider playing a series of 5 games against a chess opponent of unknown strength. If we won all 5 games, then we would have a pretty good idea that we are the better chess player. So winning each successive game actually is providing us with information about the strength of our opponent.
If we had prior knowledge about the strength of our opponent, meaning we condition on the strength of our opponent, then winning one game would not provide us with any additional information on the probability of winning the next.
But if we do not condition on the strength of our opponent, meaning that we have no prior knowledge about our opponent, then successively winning a string a games actually does give us information about the probability of winning the next game.
So the games are conditionally independent given the strength of our opponent, but not independent unconditionally.
Does unconditional independence imply conditional independence given $C$?
Ex. Popcorn and the Fire Alarm
Again, short answer is no.
You can see this in the case of some phenomenon with multiple causes.
Let $A$ be the event of the fire alarm going off.
Let $F$ be the event of a fire.
Let $C$ be the event of someone making popcorn.
Suppose that either $F$ (an actual fire) or $C$ (the guy downstairs popping corn) will result in $A$, the fire alarm going off. Further suppose that $F$ and $C$ are independent: knowing that there’s a fire $F$ doesn’t tell me anything about anyone making popcorn $C$; and vice versa.
But the probability of a fire given that the alarm goes off and no one is making any popcorn is given by $P(F|A,C^c) = 1$. After all, if the fire alarm goes off and no one is making popcorn, there can only be one explanation: there must be a fire.
So $F$ and $C$ may be independent, but they are not conditionally independent when we condition on event $A$. Knowing that nobody is making any popcorn when the alarm goes off can only mean that there is a fire.
View Lecture 5: Conditioning Continued, Law of Total Probability | Statistics 110 on YouTube.
Lecture 6: Monty Hall, Simpson’s Paradox
The Monty Hall Problem
In case you did not grow up watching way too much daytime television in America during the 70’s and early 80’s, here is Monty Hall on YouTube talking about the background of this math problem involving his popular game show, Let’s Make A Deal.
- There are three doors.
- A car is behind one of the doors.
- The other two doors have goats behind them.
- You choose a door, but before you see what’s behind your choice, Monty opens one of the other doors to reveal a goat.
- Monty offers you the chance to switch doors.
Should you switch?
Defining the problem
Let $S$ be the event of winning when you switch.
Let $D_j$ be the event of the car being behind door $j$.
Solving with a probability tree

With a probability tree, it is easy to represent the case where you condition on Monty opening door 2. Given that you initially choose door 1, you can quickly see that if you stick with door 1, you have a $\frac{1}{3}~$ chance of winning.
You have a $\frac{2}{3}~$ chance of winning if you switch.
Solving with the Law of Total Probability
This is even easier to solve using the Law of Total Probability.
\begin{align}
P(S) &= P(S|D_1)P(D_1) + P(S|D_2)P(D_2) + P(S|D_3)P(D_3)
&= 0 \frac{1}{3} + 1 \frac{1}{3} + 1 \frac{1}{3}
&= \frac{2}{3}
\end{align}
A more general solution
Let $n = 7$ be the number of doors in the game.
Let $m=3$ be the number of doors with goats that Monty opens after you select your initial door choice.
Let $S$ be the event where you win by sticking with your original door choice of door 1.
Let $C_j$ be the event that the car is actually behind door $j$.
Conditioning only on which door has the car, we have
\begin{align}
& &P(S) &= P(S|C_1)P(C_1) + \dots + P(S|C_n)P(C_n) & &\text{Law of Total
Probability}
& & &= P(C_1)
& & &= \frac{1}{7}
\end{align}
Let $M_{i,j,k}$ be the event that Monty opens doors $i,j,k$. Conditioning on Monty opening up doors $i,j,k$, we have
\begin{align}
& &P(S) &= \sum_{i,j,k} P(S|M_{i,j,k})P(M_{i,j,k}) & &\text{summed over all
i, j, k with } 2 \le i \lt j \lt k \le 7
& &\Rightarrow P(S|M_{i,j,k}) &= P(S) & &\text{by symmetry}
& & &=\frac{1}{7}
\end{align}
Note that we can now generalize this to the case where:
- there are $n \ge 3$ doors
- after you choose a door, Monty opens $m$ of the remaining doors $n-1$ doors to reveal a goat (with $1 \le m \le n-m-2$)
The probability of winning with the strategy of sticking to your initial choice is $\frac{1}{n}$, whether unconditional or conditioning on the doors Monty opens.
After Monty opens $m$ doors, each of the remaining $n-m-1$ doors has conditional probability of $\left(\frac{n-1}{n-m-1}\right) \left(\frac{1}{n}\right)$.
Since $\frac{1}{n} \lt \left(\frac{n-1}{n-m-1}\right) \left(\frac{1}{n}\right)$, you will always have a greater chance of winning if you switch.
Simpson’s Paradox
Is it possible for a certain set of events to be more (or less) probable than another without conditioning, and then be less (or more) probable with conditioning?

Assume that we have the above rates of success/failure for Drs. Hibbert and Nick for two types of surgery: heart surgery and band-aid removal.
Defining the problem
Let $A$ be the event of a successful operation.
Let $B$ be the event of treatment by Dr. Nick.
Let $C$ be the event of heart surgery.
\begin{align}
P(A|B,C) &< P(A|B^c,C) & &\text{Dr. Nick is not as skilled as Dr. Hibbert in
heart surgery}
P(A|B,C^c) &< P(A|B^c,C^c) & &\text{neither is he all that good at band-aid
removal}
\end{align}
| And yet $P(A | B) > P(A | B^c)$? |
Explaining with the Law of Total Probability
To explain this paradox, let’s try to use the Law of Total Probability.
\begin{align}
P(A|B) &= P(A|B,C)P(C|B) + P(A|B,C^c)P(C^c|B)
\text{but } P(A|B,C) &< P(A|B^c,C)
\text{and } P(A|B,C^c) &< P(A|B^c,C^c)
\end{align}
Look at $P(C|B$ and $P(C|B^c)$. These weights are what makes this paradox possible, as they are what make the inequality relation sign flip.
Event $C$ is a case of confounding
Another example
Is it possible to have events $A_1, A_2, B, C$ such that
\begin{align}
P(A_1|B) &\gt P(A_1|C) \text{ and } P(A_2|B) \gt P(A_2|C) & &\text{ …
yet…}
P(A_1 \cup A_2|B) &\lt P(A_1 \cup A_2|C)
\end{align}
Yes, and this is just another case of Simpson’s Paradox.
Note that
\begin{align} P(A_1 \cup A_2|B) &= P(A_1|B) + P(A_2|B) - P(A_1 \cap A_2|B) \end{align}
| So this is not possible if $A_1$ and $A_2$ are disjoint and $P(A_1 \cup A_2 | B) | |
| = P(A_1 | B) + P(A_2 | B)$. |
| It is crucial, therefore, to consider the intersection $P(A_1 \cap A_2 | B)$, so |
| let’s look at the following example where $P(A_1 \cap A_2 | B) \gg P(A_1 \cap |
| A_2 | C)$ in order to offset the other inequalities. |
Consider two basketball players each shooting a pair of free throws.
Let $A_j$ be the event basketball free throw scores on the $j^{th}$ try.
| Player $B$ always either makes both $P(A_1 \cap A_2 | B) = 0.8$, or misses both. |
\begin{align} P(A_1|B) = P(A_2|B) = P(A_1 \cap A_2|B) = P(A_1 \cup A_2|B) = 0.8 \end{align}
Player $C$ makes free throw shots with probability $P(A_j|C) = 0.7$, independently, so we have
\begin{align}
P(A_1|C) &= P(A_2|C) = 0.7
P(A_1 \cap A_2|C) &= P(A_1|C) P(A_2|C) = 0.49
P(A_1 \cup A_2|C) &= P(A_1|C) + P(A_2|C) - P(A_1 \cap A_2|C)
&= 2 \times 0.7 - 0.49
&= 0.91
\end{align}
And so we have our case where
\begin{align}
P(A_1|B) = 0.8 &\gt P(A_1|C) = 0.7
P(A_2|B) = 0.8 &\gt P(A_2|C) = 0.7
\text{ … and yet… }
P(A_1 \cup A_2|B) &\lt P(A_1 \cup A_2|C) ~~~~ \blacksquare
\end{align}
View Lecture 6: Monty Hall, Simpson’s Paradox | Statistics 110 on YouTube.
Lecture 7: Gambler’s Ruin & Random Variables
Gambler’s Ruin
Two gamblers $A$ and $B$ are successively playing a game until one wins all the money and the other is ruined (goes bankrupt). There is a sequence of rounds, with a one dollar bet each time. The rounds are independent events. Let $p = P(\text{A wins a certain round})$ and the inverse is $q = 1 - p$, by convention.
What is the probability that $A$ wins the entire game?
Some clarifications:
- there is a total of $N$ dollars in this closed system game (no other money comes into play)
- $A$ starts with $i$ dollars, $B$ starts with $N-i$ dollars
But where do we begin to solve this problem?
Random Walk
A random walk between two points on a number line is very similar to the Gambler’s Ruin.

How many rounds could a game last? Is it possible for the game to continue on to infinity?
Well, notice how this has a very nice recursive nature. If $A$ loses a round, the game can be seen as starting anew at $i-1$, and if he wins, the game would start anew at $i+1$. It is the same problem, but with a different starting condition.
Strategy
Conditioning on the first step is called first step analysis.
Let $P_i = P(\text{A wins the entire game|A starts with i dollars})$. Then from the Law of Total Probability, we have:
\begin{align}
P_i &= p P_{i+1} + q P_{i-1} \text{, } & &\text{where }1 \lt i \lt N-1
& & & P_0 = 0
& & & P_N = 1
\end{align}
See how this is a recursive equation? This is called a difference equation, which is a discrete analog of a differential equation.
Solving the Difference Equation
\begin{align}
P_i &= p P_{i+1} + q P_{i-1} & &
P_i &= x^i & &\text{see what happens when we guess with a power}
\Rightarrow x^i &= p x^{i+1} + q x^{i-1}
0 &= p x^2 - x + q & &\text{factoring out } x^{i-1} \text{, we are left with
a quadratic}
x &= \frac{1 \pm \sqrt{1-4pq}}{2p} & &\text{solving with the quadratic
formula}
&= \frac{1 \pm \sqrt{(2p-1)^2}}{2p} & &\text{since }1-4pq = 1-4p(1-p) =
4p^2 - 4p - 1 = (2p -1)^2
&= \frac{1 \pm (2p-1)}{2p}
&\in \left{1, \frac{q}{p} \right}
P_i &= A(1)^i + B\left(\frac{q}{p}\right)^i & &\text{if } p \neq q~~~~
\text{(general solution for difference equation)}
\Rightarrow B &= -A & &\text{from }P_0 = 1
\Rightarrow 1 &= A(1)^N + B\left(\frac{q}{p}\right)^N & &\text{from } P_N =
1
&= A(1)^N - A\left(\frac{q}{p}\right)^N
&= A\left(1-\frac{q}{p}\right)^N
\therefore P_i &=
\begin{cases}
\frac{1-\left(\frac{q}{p}\right)^i}{1-\left(\frac{q}{p}\right)^N} &
\quad \text{ if } p \neq q
\frac{i}{N} & \quad \text{ if } p = q
\end{cases}
\end{align}
Example calculations of $P_i$ over a range of $N$
Assuming an unfair game where $p=0.49$, $q=0.51$:
import math
def gamblers_ruin(i, p, q, N):
if math.isclose(p,q):
return i/N
else:
return ((1 - (q/p)**i)) / (1 - (q/p)**N)
p = 0.49
q = 1.0 - p
N = 20
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
N = 100
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
N = 200
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
And assuming a fair game where $p = q = 0.5$:
p = 0.5
q = 1.0 - p
N = 20
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
N = 100
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
N = 200
i = N/2
print("With N={} and p={}, probability that A wins all is {:.2f}".format(N, p, gamblers_ruin(i, p, q, N)))
Could the game ever continue forever on to infinity?
Recall that we have the following solution to the difference equation for the Gambler’s Ruin game:
\begin{align}
P_i &=
\begin{cases}
\frac{1-\left(\frac{q}{p}\right)^i}{1-\left(\frac{q}{p}\right)^N} &
\quad \text{ if } p \neq q
\frac{i}{N} & \quad \text{ if } p = q
\end{cases}
\end{align}
The only time you’d think the game could continue on to infinity is when $p=q$. But
\begin{align}
P(\Omega) &= 1
&= P(\text{A wins all}) + P(\text{B wins all})
&= P_i + P_{N-i}
&= \frac{i}{N} + \frac{N-i}{N}
\end{align}
The above implies that aside from the case where $A$ wins all, and the case where $B$ wins all, there is no other event in $\Omega$ to consider, hence the game can never continue on to infinity without either side winning.
This also means that unless $p=q$, you will lose your money, and the only question is how fast will you lose it.
Random Variables
Consider these statements:
\begin{align}
x + 2 &= 9
x &= 7
\end{align}
What is a variable?
- variable $x$ is a symbol that we use as a substitute for an arbitrary constant value.
What is a random variable?
- This is not a variable, but a function from the sample space $S$ to $\mathbb{R}$.
- It is a “summary” of an aspect of the experiment (this is where the randomness comes from)
Here are a few of the most useful discrete random variables.
Bernoulli Distribution
Description
A probability distribution of a random variable that takes the value 1 in the case of a success with probability $p$; or takes the value 0 in case of a failure with probability $1-p$.
A most common example would be a coin toss, where heads might be considered a success with probability $p=0.5$ if the coin is a fair.
A random variable $x$ has the Bernoulli distribution if
- $x \in {0, 1}$
- $P(x=1) = p$
- $P(x=0) = 1-p$
Notation
$X \sim \operatorname{Bern}(p)$
Parameters
$0 < p < 1 \text{, } p \in \mathbb{R}$
Probability mass function
The probability mass function $P(x)$ over possible values $x$
\begin{align}
P(x) =
\begin{cases}
1-p, &\text{ if } x = 0
p, &\text{ if } x = 1
\end{cases}
\end{align}
Expected value
\begin{align}
\mathbb{E}(X) &= 1 P(X=1) + 0 P(X=0)
&= p
\end{align}
Special case: Indicator random variables (r.v.)
\begin{align}
&X =
\begin{cases}
1, &\text{ if event A occurs}
0, &\text{ otherwise}
\end{cases}
\Rightarrow &\mathbb{E}(X) = P(A)
\end{align}
Binomial Distribution
Description
The distribution of the number of successes in $n$ independent Bernoulli trials $\operatorname{Bern}(p)$, where the chance of success $p$ is the same for all trials $n$.
Another case might be a string of indicator random variables.
Notation
$X \sim \operatorname{Bin}(n, p)$
Parameters
- $n \in \mathbb{N}$
- $p \in [0,1]$
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
from scipy.stats import binom
%matplotlib inline
plt.xkcd()
_, ax = plt.subplots(figsize=(12,8))
# a few Binomial parameters n and p
pop_sizes = [240, 120, 60, 24]
p_values = [0.2, 0.3, 0.4, 0.8]
params = list(zip(pop_sizes, p_values))
# colorblind-safe, qualitative color scheme
colors = ['#a6cee3','#1f78b4','#b2df8a','#33a02c']
for i,(n,p) in enumerate(params):
x = np.arange(binom.ppf(0.01, n, p), binom.ppf(0.99, n, p))
y = binom.pmf(x, n, p)
ax.plot(x, y, 'o', ms=8, color=colors[i], label='n={}, p={}'.format(n,p))
ax.vlines(x, 0, y, color=colors[i], alpha=0.3)
# legend styling
legend = ax.legend()
for label in legend.get_texts():
label.set_fontsize('large')
for label in legend.get_lines():
label.set_linewidth(1.5)
# y-axis
ax.set_ylim([0.0, 0.23])
ax.set_ylabel(r'$P(x=k)$')
# x-axis
ax.set_xlim([10, 65])
ax.set_xlabel('# of successes k out of n Bernoulli trials')
# x-axis tick formatting
majorLocator = MultipleLocator(5)
majorFormatter = FormatStrFormatter('%d')
minorLocator = MultipleLocator(1)
ax.xaxis.set_major_locator(majorLocator)
ax.xaxis.set_major_formatter(majorFormatter)
ax.grid(color='grey', linestyle='-', linewidth=0.3)
plt.suptitle(r'Binomial PMF: $P(x=k) = \binom{n}{k} p^k (1-p)^{n-k}$')
plt.show()
Probability mass function
\begin{align} P(x=k) &= \binom{n}{k} p^k (1-p)^{n-k} \end{align}
Expected value
\begin{align} \mathbb{E}(X) = np \end{align}
In parting…
Now think about this true statement as we move on to Lecture 3:
\begin{align}
X &\sim \operatorname{Bin}(n,p) \text{, } Y \sim \operatorname{Bin}(m,p)
\rightarrow X+Y &\sim \operatorname{Bin}(n+m, p)
\end{align}
Appendix A: Solving $P_i$ when $p=q$ using l’Hopital’s Rule
To solve for for the case where $p = q$, let $x = \frac{q}{p}$.
\begin{align}
lim_{x \rightarrow 1}{\frac{1-x^i}{1-x^N}} &=
lim_{x\rightarrow1}{\frac{ix^{i-1}}{Nx^{N-1}}} &\text{ by l’Hopital’s Rule}
&= \frac{i}{N}
\end{align}
View Lecture 7: Gambler’s Ruin and Random Variables | Statistics 110 on YouTube.
Lecture 8: Random Variables and Their Distributions
Two Basic Types of Random Variables
There are two basic types of random variables.
-
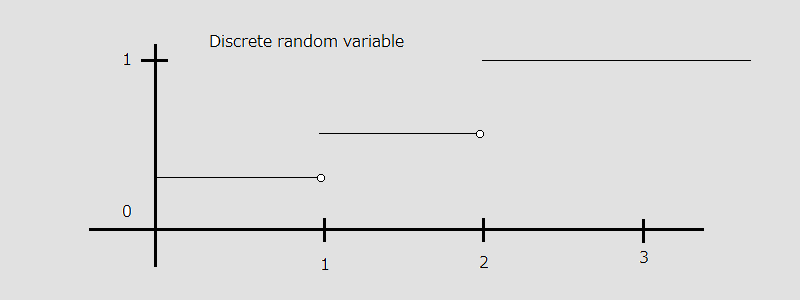
Discrete random variables are random variables whose values can be enumerated, such as $a_1, a_2, \dots , a_n$. Here, discrete does not necessarily mean only integers.
-
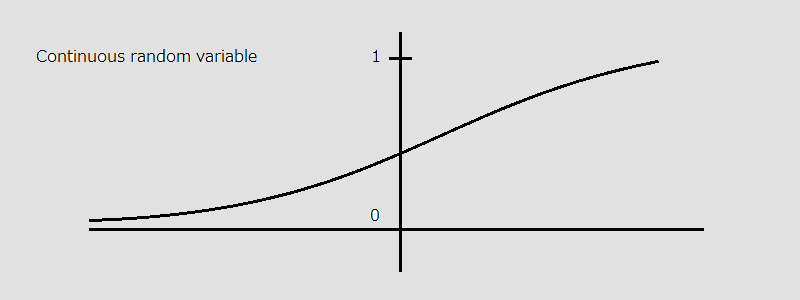
Continuous random variables, on the other hand, can take on values in $\mathbb{R}$.
Note that there are other types that might mix the two definitions.
Cumulative distribution function
Given $X \le x$ is an event, and a function $F(x) = P(X \le x)$.
Then $F$ is known as the cumulative distribution function (CDF) of $X$. In contrast with the probability mass function, the CDF is more general, and is applicable for both discrete and continuous random variables.
Probability mass function
The probability mass function (PMF) is $P(X=a_j)$, for all $\text{j}$. A pmf must satisfy the following conditions:
\begin{align} P_j &\ge 0 \newline \sum_j P_j &= 1 \end{align}
In practice, using a PMF is easier than a CDF, but a PMF is only applicable in the case of discrete random variables only.
Revisiting the Binomial Distribution $\operatorname{Bin}(n,p)$
$X \sim \operatorname{Bin}(n, p)$, where
- $n$ is an integer greater than 0
- $p$ is between 0.0 and 1.0
Here are a few different ways to explain the Binomial distribution.
Explanation with a story
$X$ is the number of successes in $n$ independent $\operatorname{Bern}(p)$ trials.
Explanation using sum of indicator random variables
\begin{align}
&X = X_1 + X_2 + \dots + X_j
& &\text{where } X_j =
\begin{cases}
1, &\text{if } j^{\text{th}} \text{ trial succeeds} \newline
0, &\text{ otherwise }
\end{cases}
& & &\text{and } X_1, X_2, \dots , X_j \text{ are i.i.d }
\operatorname{Bern}(p)
\end{align}
Explanation using a probability mass function
\begin{align} P(X=k) = \binom{n}{k} p^k q^{n-k} \text{, where } q = 1 - p \text{ and } k \in {0,1,2, \dots ,n} \end{align}
A probability mass function sums to 1. Note that
\begin{align}
\sum_{k=0}^n \binom{n}{k} p^k q^{n-k} &= (p + q)^n & &\text{by the Binomial Theorem}
&= (p + 1 - p)^n
&= 1^n
&= 1
\end{align}
so the explanation by PMF holds. By the way, it is this relation to the
Binomial Theorem that this
distribution gets its name.
Sum of Two Binomial Random Variables
Recall that we left Lecture 7 with this parting thought:
\begin{align} & X \sim \operatorname{Bin}(n,p) \text{, } Y \sim \operatorname{Bin}(m,p) \rightarrow X+Y \sim \operatorname{Bin}(n+m, p) \end{align}
Let’s see how this is true by using the three explanation approaches we used earlier.
Explanation with a story
$X$ and $Y$ are functions, and since they both have the same sample space $S$ and the same domain.
$X$ is the number of successes in $n \operatorname{Bern}(p)$ trials.
$Y$ is the number of successes in $m \operatorname{Bern}(p)$ trials.
$\therefore X + Y$ is simply the sum of successes in $n+m \operatorname{Bern}(p)$ trials.
Explanation using a sum of indicator random variables
\begin{align}
&X = X_1 + X_2 + \dots + X_n, ~~~~ Y = Y_1 + Y_2 + \dots + Y_m
&\Rightarrow X+Y = \sum_{i=1}^n X_j + \sum_{j=1}^m Y_j \text{, which is } n + m \text{ i.i.d. } \operatorname{Bern}(p)
&\Rightarrow \operatorname{Bin}(n + m, p)
\end{align}
Explanation using a probability mass function
We start with a PMF of the convolution $X+Y=k$
\begin{align} P(X+Y=k) &= \sum_{j=0}^k P(X+Y=k|X=j)P(X=j) & &\text{wishful thinking, assume we know } x \text{ and apply LOTP} \newline &= \sum_{j=0}^k P(Y=k-j|X=j) \binom{n}{j} p^j q^{n-j} & &\text{… but since events }Y=k-j \text{ and } X=j \text{ are independent}\newline &= \sum_{j=0}^k P(Y=k-j) \binom{n}{j} p^j q^{n-j} & &P(Y=k-j|X=j) = P(Y=k-j) \newline &= \sum_{j=0}^k \binom{m}{k-j} p^{k-j} q^{m-k+j}~~~ \binom{n}{j} p^j q^{n-j} \newline &= p^k q^{m+n-k} \underbrace{\sum_{j=0}^k \binom{m}{k-j}\binom{n}{j}}_{\text{Vandermonde’s Identity}} & &\text{see Lecture 2, Story Proofs, Ex.3} \newline &= \binom{m+n}{k} p^k q^{m+n-k} ~~~~ \blacksquare \end{align}
Hypergeometric Distribution
A common mistake in trying to use the Binomial distribution is forgetting that
- the trials are independent
- they have the same probability of success
Example: How Many Aces in a 5-card Hand?
A 5-card hand out of a standard 52-card deck of playing cards, what is the the distribution (PMF or CDF) of the number of aces.
Let $X = (\text{# of aces})$.
Find $P(X=k)$ where $x \in \text{{0,1,2,3,4}}$. At this point, we can conclude that the distribution is not Binomial, as the trials are not independent.
The PMF is given by \begin{align} P(X=k) &= \frac{\binom{4}{k}\binom{48}{5-k}}{\binom{52}{5}} \end{align}
Example: Sampling White/Black Marbles
Suppose we have a total of $b$ black and $w$ white marbles. Pick a random sample of $n$ marbles. What is the distribution on the # white marbles?
\begin{align} P(X=k) &= \frac{\binom{w}{k}\binom{b}{n-k}}{\binom{w+b}{n}} \end{align}
The distribution in the examples above is called the Hypergeometric distribution. In the hypergeometric distribution, we sample without replacement, and so the trials cannot be independent.
Note that when the total number of items in our sample is exceedingly large, it becomes highly unlikely that we would choose the same item more than once. Therefore, it doesn’t matter if you are sampling with replacement or without, suggesting that in this case the hypergeometric behaves as the binomial.
Is the Hypergeometric distribution a valid PMF?
Is the hypergeometric non-negative?
Yes, obviously.
Does the PMF sum to 1?
\begin{align} P(X=k) &= \sum_{k=0}^w \frac{\binom{w}{k}\binom{b}{n-k}}{\binom{w+b}{n}} \newline &= \frac{1}{\binom{w+b}{n}} \sum_{k=0}^w \binom{w}{k}\binom{b}{n-k} & &\text{since }\binom{w+b}{n} \text{ is constant} \newline &= \frac{1}{\binom{w+b}{n}} \binom{w+b}{n} & &\text{by Vandermonde’s Identity } \newline &= 1 ~~~~ \blacksquare \end{align}
Appendix A: Independent, Identically Distributed
A sequence of random variables are independent and identically distributed (i.i.d) if each r.v. has the same probability distribution and all are mutually independent.
Think of the Binomial distribution where we consider a string of coin flips. The probability $p$ for head’s is the same across all coin flips, and seeing a head (or tail) in a previous toss does not affect any of the coin flips that come afterwards.
Lecture 9: Expectation, Indicator Random Variables, Linearity
More on Cumulative Distribution Functions
A CDF: $F(x) = P(X \le x)$, as a function of real $x$ has to be
- non-negative
- add up to 1
In the following discrete case, it is easy to see how the probability mass function (PMF) relates to the CDF:
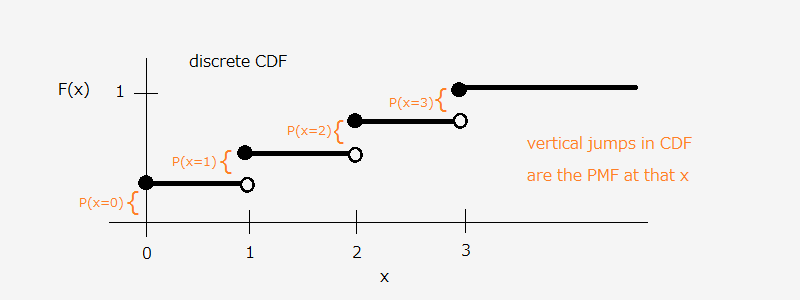
Therefore, you can compute any probability given a CDF.
Ex. Find $P(1 \lt x \le 3)$ using CDF $F$.
\begin{align} & &P(x \le 1) + P(1 \lt x \le 3) &= P(x \le 3) \newline & &\Rightarrow P(1 \lt x \le 3) &= F(3) - F(1) \end{align}
Note that while we don’t need to be so strict in the continuous case, for the discrete case you need to be careful about the $\lt$ and $\le$.
Properties of CDF
A function $F$ is a CDF iff the following three conditions are satisfied.
- increasing
- right-continuous (function is continuous as you approach a point from the right)
- $F(x) \rightarrow 0 \text{ as } x \rightarrow - \infty$, and $F(x) \rightarrow 1 \text{ as } x \rightarrow \infty$.
Independence of Random Variables
$X, Y$ are independent r.v. if
\begin{align} \underbrace{P(X \le x, Y \le y)} &= P(X \le x) P(Y \le y) & &\text{ for all x, y in the continuous case} \newline \underbrace{P(X=x, Y=y)}_{\text{joint PMF}} &= P(X=x) P(Y=y) & &\text{ for all x, y in the discrete case} \end{align}
Averages of Random Variables (mean, Expected Value)
A mean is… well, the average of a sequence of values.
\begin{align} 1, 2, 3, 4, 5, 6 \rightarrow \frac{1+2+3+4+5+6}{6} = 3.5 \end{align}
In the case where there is repetition in the sequence
\begin{align}
1,1,1,1,1,3,3,5 \rightarrow & \frac{1+1+1+1+1+3+3+5}{8}
& \dots \text{ or } \dots
& \frac{5}{8} ~~ 1 + \frac{2}{8} ~~ 3 + \frac{1}{8} ~~ 5 & &\quad \text{ …
weighted average}
\end{align}
where the weights are the frequency (fraction) of the unique elements in the sequence, and these weights add up to 1.
Expected value of a discrete r.v. $X$
\begin{align} \mathbb{E}(X) = \sum_{x} \underbrace{x}{\text{value}} ~~ \underbrace{P(X=x)}{\text{PMF}} ~& &\quad \text{ … summed over x with } P(X=x) \gt 0 \end{align}
Expected value of $X \sim \operatorname{Bern}(p)$
\begin{align}
\text{Let } X &\sim \operatorname{Bern}(p)
\mathbb{E}(X) &= \sum_{k=0}^{1} k P(X=k)
&= 1 ~~ P(X=1) + 0 ~~ P(X=0)
&= p
\end{align}
Expected value of an Indicator Variable
\begin{align}
X &=
\begin{cases}
1, &\text{ if A occurs}
0, &\text{ otherwise }
\end{cases}
\therefore \mathbb{E}(X) &= P(A)
\end{align}
Notice how this lets us relate (bridge) the expected value $\mathbb{E}(X)$ with a probability $P(A)$.
Average of $X \sim \operatorname{Bin}(n,p)$
There is a hard way to do this, and an easy way.
First the hard way:
\begin{align}
\mathbb{E}(X) &= \sum_{k=0}^{n} k \binom{n}{k} p^k (1-p)^{n-k}
&= \sum_{k=0}^{n} n \binom{n-1}{k-1} p^k (1-p)^{n-k} & &\text{from Lecture
2, Story proofs, ex. 2, choosing a team and president}
&= np \sum_{k=0}^{n} n \binom{n-1}{k-1} p^{k-1} (1-p)^{n-k}
&= np \sum_{j=0}^{n-1} \binom{n-1}{j} p^j(1-p)^{n-1-j} & &\text{letting }
j=k-1 \text{, which sets us up to use the Binomial Theorem}
&= np
\end{align}
Now, what about the easy way?
Linearity of Expected Values
Linearity is this:
\begin{align}
\mathbb{E}(X+Y) &= \mathbb{E}(X) + \mathbb{E}(Y) & &\quad \text{even if X and
Y are dependent}
\mathbb{E}(cX) &= c \mathbb{E}(X)
\end{align}
Expected value of Binomial r.v using Linearity
Let $X \sim \operatorname{Bin}(n,p)$. The easy way to calculate the expected value of a binomial r.v. follows.
Let $X = X_1 + X_2 + \dots + X_n$ where $X_j \sim \operatorname{Bern}(P)$.
\begin{align}
\mathbb{E}(X) &= \mathbb{E}(X_1 + X_2 + \dots + X_n)
\mathbb{E}(X) &= \mathbb{E}(X_1) + \mathbb{E}(X_2) + \dots + \mathbb{E}(X_n) &
&\quad \text{by Linearity}
\mathbb{E}(X) &= n \mathbb{E}(X_1) & &\quad \text{by symmetry}
\mathbb{E}(X) &= np
\end{align}
Expected value of Hypergeometric r.v.
Ex. 5-card hand $X=(# aces)$. Let $X_j$ be the indicator that the $j^{th}$ card is an ace.
\begin{align}
\mathbb{E}(X) &= \mathbb{E}(X_1 + X_2 + X_3 + X_4 + X_5)
&= \mathbb{E}(X_1) + \mathbb{E}(X_2) + \mathbb{E}(X_3) + \mathbb{E}(X_4) +
\mathbb{E}(X_5) & &\quad \text{by Linearity}
&= 5 ~~ \mathbb{E}(X_1) & &\quad \text{by symmetry}
&= 5 ~~ P(1^{st} \text{ card is ace}) & &\quad \text{by the Fundamental
Bridge}
&= \boxed{\frac{5}{13}}
\end{align}
Note that when we use linearity in this case, the individual probabilities are weakly dependent, in that the probability of getting an ace decreases slightly; and that if you already have four aces, then the fifth card cannot possibly be an ace. But using linearity, we can nevertheless quickly and easily compute $\mathbb{E}(X_1 + X_2 + X_3 + X_4 + X_5)$.
Geometric Distribution
Description
The Geometric distribution comprises a series of independent $\operatorname{Bern}(p)$ trials where we count the number of failures before the first success.
Notation
$X \sim \operatorname{Geom}(p)$.
Parameters
$0 < p < 1 \text{, } p \in \mathbb{R}$
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import (MultipleLocator, FormatStrFormatter,
AutoMinorLocator)
from scipy.stats import geom
%matplotlib inline
plt.xkcd()
_, ax = plt.subplots(figsize=(12,8))
# seme Geometric parameters
p_values = [0.2, 0.5, 0.75]
# colorblind-safe, qualitative color scheme
colors = ['#1b9e77', '#d95f02', '#7570b3']
for i,p in enumerate(p_values):
x = np.arange(geom.ppf(0.01, p), geom.ppf(0.99, p))
pmf = geom.pmf(x, p)
ax.plot(x, pmf, 'o', color=colors[i], ms=8, label='p={}'.format(p))
ax.vlines(x, 0, pmf, lw=2, color=colors[i], alpha=0.3)
# legend styling
legend = ax.legend()
for label in legend.get_texts():
label.set_fontsize('large')
for label in legend.get_lines():
label.set_linewidth(1.5)
# y-axis
ax.set_ylim([0.0, 0.9])
ax.set_ylabel(r'$P(X=k)$')
# x-axis
ax.set_xlim([0, 20])
ax.set_xlabel('# of failures k before first success')
# x-axis tick formatting
majorLocator = MultipleLocator(5)
majorFormatter = FormatStrFormatter('%d')
minorLocator = MultipleLocator(1)
ax.xaxis.set_major_locator(majorLocator)
ax.xaxis.set_major_formatter(majorFormatter)
ax.xaxis.set_minor_locator(minorLocator)
ax.grid(color='grey', linestyle='-', linewidth=0.3)
plt.suptitle(r'Geometric PMF: $P(X=k) = pq^k$')
plt.show()
Probability mass function
Consider the event $A$ where there are 5 failures before the first success. We could notate this event $A$ as $\text{FFFFFS}$, where $F$ denotes failure and $S$ denotes the first success. Note that this string must end with a success. So, $P(A) = q^5p$.
And from just this, we can derive the PMF for a geometric r.v.
\begin{align}
P(X=k) &= pq^k \text{, } k \in {1,2, \dots }
\sum_{k=0}^{\infty} p q^k &= p \sum_{k=0}^{\infty} q^k
&= p ~~ \frac{1}{1-q} & &\quad \text{by the geometric series where } |r| < 1
&= \frac{p}{p}
&= 1 & &\quad \therefore \text{ this is a valid PMF}
\end{align}
Expected value
So, the hard way to calculate the expected value $\mathbb{E}(X)$ of a $\operatorname{Geom}(p)$ is
\begin{align}
\mathbb{E}(X) &= \sum_{k=0}^{\infty} k p q^k
&= p \sum_{k=0}^{\infty} k q^k
\text{ now … } \sum_{k=0}^{\infty} q^k &= \frac{1}{1-q} & &\quad \text{by
the geometric series where |q| < 1}
\sum_{k=0}^{\infty} k q^{k-1} &= \frac{1}{(1-q)^2} & &\quad \text{by
differentiating with respect to k}
\sum_{k=0}^{\infty} k q^{k} &= \frac{q}{(1-q)^2}
&= \frac{q}{p^2}
\text{ and returning, we have … } \mathbb{E}(X) &= p ~~ \frac{q}{(p^2}
&= \frac{q}{p} & &\quad \blacksquare
\end{align}
And here is the story proof, without using the geometric series and derivatives:
Again, we are considering a series of independent Bernoulli trials with probability of success $p$, and we are counting the number of failures before getting the first success.
Similar to doing a first step analysis in the case of the Gambler’s Ruin, we look at the first case where we either:
- get a heads (success) on the very first try, meaning 0 failures
- or we get 1 failure, but we start the process all over again
Remember that in the case of a coin flip, the coin has no memory.
Let $c=\mathbb{E}(X)$.
\begin{align}
c &= 0 ~~ p + (1 + c) ~~ q
&= q + qc
c - cq &= q
c (1 - q) &= q
c &= \frac{q}{1-q}
&= \frac{q}{p} & &\quad \blacksquare
\end{align}
